A few weeks ago, in another LinkedIn article, I compared stock management in your warehouse to your freezer at home. You decide which products to store and how much. Maybe you can buy smaller quantities of some products so that you have more space for others. But how do you determine the order size for purchasing or production?
For your freezer, you do so on “gut” feeling. It probably only concerns a few dozen of items and you consume them yourself, which makes it easily manageable, although we often also have to throw away food of which we bought too much. In a company, the purchaser is often not the person who actually uses the product. Often the user is the customer, or the production department. The purchaser therefore already has less “feeling” about a product. Moreover, it usually concerns hundreds, and often thousands or even tens of thousands of references. In that case, you can no longer decide on experience and feeling how much you will buy of each item.
The question is whether they also take into account how much we actually need for our customer and what are the costs of keeping inventory?
In most ERP systems, a lot size can be defined, to ensure that, when you place a purchase order or a production order, you get a proposal of how many pieces, litres or kg you have to order or produce. But when creating a new article, you will be asked to enter an order size in your ERP system. How do you go about determining this lot size? Often your supplier or your production manager will propose some value, for example a full pallet or a minimum number of hours of production. In doing so, they will mainly take into account the costs of preparing an order or the changeover costs. The question is whether they also take into account how much we actually need for our customer and what are the costs of keeping inventory?
As a manager, it is our duty to take all relevant costs into account when determining lot sizes. A formula that is very useful and that I often use myself, is the EOQ formula, developed over a hundred years ago by Ford W. Harris in 1913! Since then, many extensions have been made to this formula, but the basis still stands. EOQ stands for Economic Order Quantity and weighs costs of keeping stock on the one hand and set-up or order costs on the other.
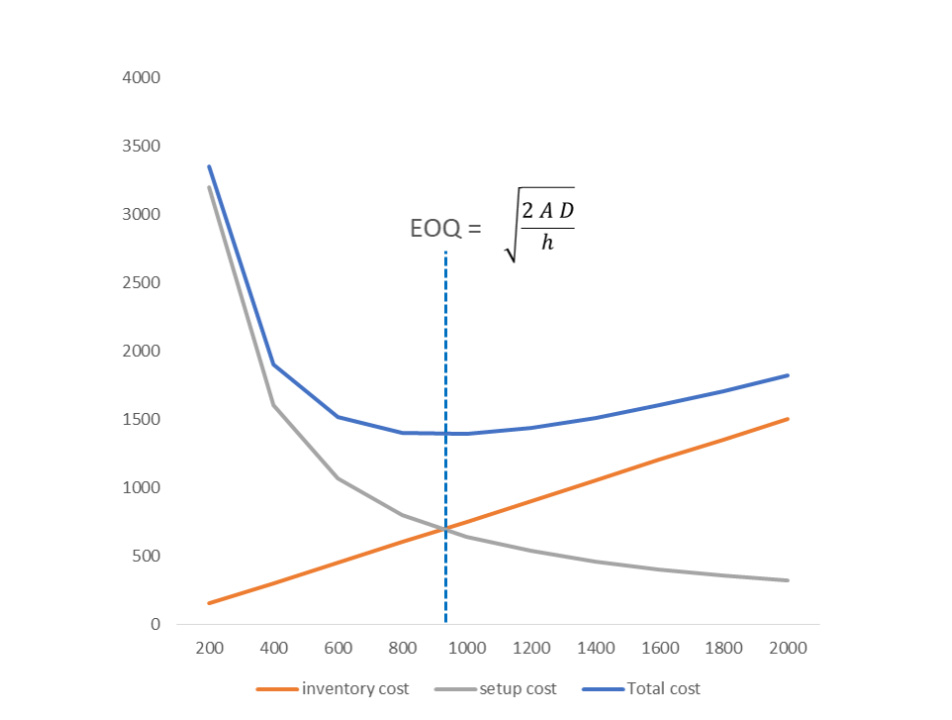
We can determine inventory costs by multiplying a holding cost per unit x the average number of units in stock (in case of regular demand, this will be half of the order size). The holding cost includes all costs you incur annually to keep the item in stock, for example rent, insurance but also the opportunity cost of tying up capital instead of using it for something else. The larger the order size and therefore the average stock, the higher inventory costs will be.
On the other hand, set-up or order costs decrease as the order size increases. If the annual demand is D and the order size is Q, then D / Q is the number of times per year that we will order or produce. The changeover or order costs are therefore D / Q x A, where A is a fixed cost per order, taking into account extra maintenance personnel, administration, extra scrap, etc.
Total replenishment cost is therefore: D / Q x A + h x Q / 2
The graph below shows inventory costs, set-up costs and the sum of both.
I am going to spare you the mathematical theory to determine the optimal value of Q. But if we minimize the above formula, the optimal order size Q is:



Leave A Comment